数据结构

简介

• 什么是数据类型？

  • 现实世界中各种类型的信息，在计算机中可以用各种类型的数据表示，比如文本、图片。
  • 从机器语言的角度来看，各种类型的数据，都是存储成二进制格式，也就是一些 bits 。
  • 从汇编语言的角度来看，以 bit 为单位处理数据比较麻烦，通常以 byte 为单位处理数据。
    • 为了方便人类阅读，通常将每个 byte 的数据，表示为十六进制数字，取值范围为 00~FF 。
    • 也可以将每个 byte 的数据，表示为十进制数字，取值范围为 0~255 。
  • 从高级语言的角度来看，为了方便人类阅读数据，byte 数据可以表示为多种形式，比如十进制整数、十进制小数、英文字母。
    • 比如 C 语言的 int、float、char 数据类型，就是以不同形式表示数据，这些数据在底层都是存储成二进制格式。
    • 总之，机器语言、汇编语言通常不考虑数据类型，而高级语言通常划分了多种数据类型。

• 什么是数据结构？

  • 数据类型，是研究单个变量，如何存储、表示。
  • 数据结构，是研究由多个变量（又称为元素、节点）组成的一个集体，如何存储、表示。
  • 研究数据结构时，不一定严格要求其中元素的数据类型。
    • 比如 C 语言的数组，要求每个元素采用相同的数据类型。
    • 比如 Python 的列表，允许每个元素采用不同的数据类型。

• 人们发明了多种数据结构，按照是否有序，可以分为两大类：

  • 线性结构
    • ：所有元素，可以按照某种顺序，在逻辑上排列成一条线。又称为线性表。
    • 通常按照顺序，给每个元素分配一个序号，从 0 开始递增。
    • 线性结构是指逻辑上有序。在存储时，不一定有序。比如链表中的所有元素，分散存储，但逻辑上有序。
    • 数组、栈、队列、链表，都属于线性结构。
  • 非线性结构
    • 比如树形结构，每个元素只有一个父元素，但可以有一个或多个子元素。
    • 比如图形结构，任意两个元素之间都可能建立联系。因此访问一个元素之后，访问的下一个元素可能是任一元素。

数组

• 数组（array）的原理：

  • 将一组元素，存储在一组地址连续的存储空间中。
  • 每个元素占用的存储空间，大小相同，都是 Size 个字节。
  • 记录第 0 个元素的存储地址，称为 first_address 。

• 特点：

  • 连续存储
  • 线性结构
    • 所有元素，可以按照存储顺序，在逻辑上排列成一条线。
  • 支持正序访问
    • 用户可以先访问 first_address ，里面存储的是第 0 个元素。然后访问下一块相邻的存储地址，里面存储的是第 1 个元素。然后访问下一块相邻的存储地址，里面存储的是第 2 个元素。以此类推。
    • 因此，用户可以按照 0 -> 1 -> 2 的顺序，依次访问所有元素。
  • 支持随机访问
    • 用户可以不遵守顺序，直接访问任一元素。
    • 假设用户想访问第 i 个元素，则可以计算出第 i 个元素的存储地址为 first_address + i * Size ，然后访问该地址。

• 例如 C 语言中，可使用数组：

  int array[10] = {0,1,2,3};  // 创建一个数组，可以存储 10 个 int 类型的元素，并写入几个元素
  printf("%p\n", array);      // 输出为：0x7fff7185d120 。因为数组名 array 用于记录该数组的首地址
  printf("%d\n", *array);     // 输出为：0 。因为 *array 等价于 array[0] ，表示数组中第 0 个元素
  printf("%d\n", *(array+1)); // 输出为：1 。因为 *(array+1) 等价于 array[1] ，表示数组中第 1 个元素
  

• 性能：

  • 用户可以直接读、写数组中第 i 个元素。因此读操作、写操作的时间复杂度为 O(1) 。
  • 假设数组包含 n 个元素，用户想知道哪个元素的取值等于 v ，则需要遍历数组中所有元素，检查每个元素的值。因此时间复杂度为 O(n) 。
    • 数组、栈、队列、链表，都属于线性结构，查询一个元素的时间复杂度为 O(n) 。

栈

• 栈（stack）的原理：

  • 将一组元素，存储在一组地址连续的存储空间中。
  • 记录最后一个元素（称为栈顶元素）的存储地址。

• 提供 stack 这种数据结构的程序，一般允许用户执行以下几种操作：

  • 入栈（push）
    • ：将一个新元素，加入 stack ，成为新的栈顶元素。
  • 出栈（pop）
    • ：将栈顶元素，从 stack 取出，并读取该元素的值。同时，倒数第二个元素，会成为新的栈顶元素。
    • 打个比方，stack 像将多本书堆成一叠。用户要么在顶部加一本书，要么拿走顶部的那本书。用户不能操作非顶部的书。
    • push、pop 属于基础操作，时间复杂度为 O(1) 。
  • peek
    • ：读取栈顶元素的值，但不将它出栈。
    • 程序不一定支持 peek 。有的程序，必须将栈顶元素出栈，才能读取其值。
  • is_empty
    • ：检查 stack 是否为空，即不存在元素。
    • 如果 stack 为空，则 pop、peek 操作会失败，甚至可能导致程序 bug 。
    • 为了避免这种问题，有的程序会在每次 pop、peek 之前，自动检查 stack 是否为空。如果为空，则不进行 pop、peek 。
  • is_full
    • ：检查 stack 是否写满。
    • 创建一个 stack 时，一般要限制它的最大容量。如果 stack 写满了元素，则 push 操作会失败，甚至可能导致程序 bug 。
    • 为了避免这种问题，有的程序会在每次 push 之前，自动检查 stack 是否写满。如果写满，则不进行 push 。

• 特点：

  • 连续存储
  • 线性结构
  • 支持倒序访问
    • 用户执行一次出栈，就会取出栈顶元素。再执行一次出栈，就会读取下一个元素。
    • 这里采用的是倒序，又称为 LIFO（Last In First Out，后进先出），最后一个被写入 stack 的元素，会最先出栈、被读取到。
    • 读取数组中的元素时，不会修改数组。而读取 stack 中的元素时，需要出栈，删除栈顶元素。如果将 stack 中的所有元素出栈，则该 stack 内容为空。
  • 不支持随机访问
    • stack 中，每个元素占用的存储空间，大小不一定相同。因此用户想访问第 i 个元素时，不能计算出其存储地址。
    • 从技术上来说，如果用户记录了每个元素的存储地址，就支持随机访问。但 stack 是一种基础的数据结构，为了减少开销，只记录最后一个元素的存储地址。

队列

• 队列（queue）的原理：

  • 将一组元素，存储在一组地址连续的存储空间中。
  • 记录第一个元素（称为队首）的存储地址。
  • 记录最后一个元素（称为队尾）的存储地址。

• 提供 queue 这种数据结构的程序，一般允许用户执行以下几种操作：

  • 入队（enqueue）
    • ：将一个新元素，加入 queue ，成为新的队尾元素。
  • 出队（dequeue）
    • ：将队尾元素，从 queue 取出，并读取该元素的值。
    • 打个比方，queue 像一根水管，只能从一端塞入乒乓球，球会从另一端出来。
  • peek
    • ：读取队尾元素的值，但不将它出队。
  • is_empty
  • is_full
    • 创建一个 queue 时，一般要限制它的最大容量，最多存储 N 个元素。如果 queue 写满了元素，则 enqueue 操作会失败，甚至可能导致程序 bug 。
    • 为了避免这种问题，有的程序会在每次 enqueue 之前，自动检查 queue 是否写满。如果写满，则不进行 enqueue 。
    • 另一种方案是，如果 queue 写满，则每次 enqueue 之前，自动 dequeue 一个元素，从而腾出空间。

• 特点：

  • 连续存储
  • 线性结构
  • 支持正序访问
    • 这里采用的顺序是正序，又称为先进先出（First-In First-Out ，FIFO），最先被写入队列的元素，会最出队、被读取到。
  • 不支持随机访问

• 队列这种数据结构，存在几种变体：

  • 双端队列
    • ：队列的两端，都可以写入元素、取出元素。因此不遵循 FIFO 顺序。
  • 循环队列
    • ：让队尾元素的下一个元素，指向队首元素。这样队列首尾相连，在逻辑上形成一个圆圈。
  • 优先级队列
    • ：给每个元素设置一个优先级（priority），取值范围为 0~100 。每次出队时，找出当前优先级最高的元素。
      • 如果只有一个元素的优先级最高，则取出该元素。
      • 如果有多个元素的优先级最高且相等，则按照 FIFO 顺序，取出这些元素中最早入队的那个元素。

链表

• 链表（linked list）的原理：

  • 将一组元素，每个元素存储在任意地址的存储空间。
  • 每个元素中，不仅记录该元素的值，还要记录下一个元素的存储地址。
  • 记录第一个元素的存储地址。

• 特点：

  • 分散存储
    • 数组中，各个元素存储在一组地址连续的存储空间中，称为连续存储、线性存储。
    • 链表中，各个元素存储在任意地址的存储空间中，称为分散存储、链式存储。
    • 因为分散存储，链表具有以下优点：
      • 数组只能容纳固定个元素，因为需要事先分配连续的存储地址。而链表可以容纳任意个元素，可以随时增加、删除元素。
      • stack 只能在末尾增加、删除元素。而链表可以在任意第 i 个元素之后，增加、删除元素。
  • 线性结构
  • 支持正序访问
    • 用户可以先访问 first_address ，里面存储了第 0 个元素的值、第 1 个元素的地址。然后用户访问第 1 个元素的地址，得知第 1 个元素的值、第 2 个元素的地址。以此类推。
    • 因此，用户可以按照 0 -> 1 -> 2 的顺序，依次访问所有元素。这称为单向链表。
  • 不支持随机访问

• 例如 C 语言中，可使用 struct 实现链表：

  #include <stdio.h>
  #include <stdlib.h>
  
  typedef struct Node{    // 定义一个结构体，表示链表中的一个节点
      int data;           // 记录当前节点的值，可以是任意取值
      struct Node *next;  // 用一个指针，记录下一个节点的地址，像一个链接
      // struct Node *last; // 如果加一个指针，记录上一个节点的地址，则变成了双向链表
  } Node;
  
  int main(void){
      Node *n0 = malloc(sizeof(Node));  // 创建第 0 个节点
      n0->data = 10;
      n0->next = NULL;  // 给指针默认赋值为 NULL ，因为此时还不存在下一个节点
  
      Node *n1 = malloc(sizeof(Node));  // 创建第 1 个节点
      n1->data = 11;
      n1->next = NULL;
      n0->next = n1;    // 记录 n1 的地址，作为 n0 的下一个节点
  
      Node *n2 = malloc(sizeof(Node));  // 创建第 2 个节点
      n2->data = 12;
      n2->next = NULL;
      n1->next = n2;    // 记录 n2 的地址，作为 n1 的下一个节点
  
      Node *head = n0;      // 创建一个 head 变量，用于记录第一个节点，表示链表的访问入口
      Node *current = head; // 创建一个 current 变量，用于记录当前访问的一个节点
      while (current != NULL) {          // 通过循环，依次访问链表中的各个节点
          printf("%d\n", current->data); // 获取当前节点的值
          current = current->next;       // 获取下一个节点的地址
      }
  
      return 0;
  }
  

• 链表这种数据结构，存在几种变体：

  • 双向链表
    • ：每个元素中，不仅记录下一个元素的地址，还记录上一个元素的地址，从而可以按两种方向遍历所有元素。
  • 循环链表
    • ：最后一个元素中，记录的下一个元素，是第一个元素。这样链表首尾相连，在逻辑上形成一个圆圈。

树

• 树（tree）这种数据结构，看起来像树，像三角形。

  • 一个树形结构，包含多个节点。这些节点在逻辑上分层放置，同层的各个节点放在同样高度。
  • 一个上层节点，与一个下层节点，可以通过一条线连接（称为一条边），代表存在联系。此时前者称为父节点，后者称为子节点。

• 如下图：

  

  • 最上层只有一个节点，它不存在父节点，而是担任其它节点的父节点、祖父节点，因此它称为根节点。
    • 除了根节点以外，其它节点都有且仅有一个父节点。
  • 如果一个节点，不存在子节点，则称为叶子节点（leaf nodes）。
    • 非叶子节点，又称为内部节点，因为被子节点包围了。
  • 一个节点，存在的子节点数量，称为该节点的度数（degree）。
    • 叶子节点的 degree 为 0 。
    • 树中所有节点的最大 degree ，称为该树的阶数（order）。
  • 节点的路径（path）：指从根节点，走到该节点，需要依次经过哪些节点。
  • 节点的深度（depth）：指从根节点，走到该节点，需要经过几条边。
    • 例如，根节点的深度为 0 。
    • 一个节点的深度，等于其路径中的节点数减一 。
  • 节点的高度（height）：指从叶子节点，往上走到该节点，需要经过几条边。
    • 例如，叶子节点的高度为 0 。
    • 树中所有节点的最大 height （也就是根节点的 height ），称为该树的高度。

二叉树

如果树形结构中，每个节点最多存在两个子节点，则称为二叉树。

• 对于每个父节点而言，左侧的子孙节点，称为左子树。右侧的子孙节点，称为右子树。

二叉树可细分为几类：

• 满二叉树（Full Binary Tree）
  • ：内部节点都拥有两个子节点。
  • 只存在根节点时，也属于满二叉树。
• 完美二叉树（Perfect Binary Tree）
  • ：属于满二叉树，且叶子结点都位于最底一层，即深度相同。
• 完全二叉树（Complete Binary Tree）
  • ：叶子结点都位于最底一层，且集中在左侧。
  • 完全二叉树相当于完美二叉树去掉了最底一层的右侧部分叶子节点。
  • 例如上图属于完全二叉树，不属于满二叉树、完美二叉树。
• 平衡二叉树（Balanced Binary Tree）
  • ：在同一个父节点下，左子树与右子树的高度差不超过 1 。
• 堆（heap）
  • ：一种排序方案，与优先级队列相似。它采用一个完全二叉树，对所有节点进行排序，然后读取根节点的值。
  • 根据排序方向，可将堆分为两种：
    • 最大堆：根节点的值，是所有节点中的最大值。
    • 最小堆：根节点的值，是所有节点中的最小值。
  • 另外，C 语言中，动态分配内存的区域也称为堆（heap），它采用链表这种数据结构，记录各块内存空间的地址。

遍历

如何遍历二叉树中所有节点（每个节点只访问一次，相当于变为线性结构）？可采用多种算法：

• 层序遍历（level order traversal）
  • ：从上到下逐层遍历，每层从左到右遍历。
  • 上图的遍历顺序是 abcdef 。
• 前序遍历（preorder traversal）
  • ：先访问父节点，再访问左子树的所有节点，最后访问右子树的所有节点。
    • 前序是指父节点最先访问。
    • 对于子树则递归遍历。
  • 上图的遍历顺序是 abdecf 。
• 中序遍历（inorder traversal）
  • ：先访问左子树，再访问父节点，最后访问右子树。
  • 上图的遍历顺序是 dbeafc 。
• 后序遍历（postorder traversal）
  • ：先访问左子树，再访问右子树，最后访问父节点。
  • 上图的遍历顺序是 debfca 。

Python 代码示例：

class Node:
    def __init__(self, name, data=None, left=None, right=None):
        self.name  = name   # 节点名，必须指定
        self.data  = data   # 节点存储的数据，默认为空
        self.left  = left   # 左子节点，默认为空
        self.right = right  # 右子节点，默认为空
    def __repr__(self):
        return "Node('{}')".format(self.name)

def preorder(node):
    """ 前序遍历 """
    if not node:
        return []
    result = []
    result.append(node)
    result.extend(preorder(node.left))
    result.extend(preorder(node.right))
    return result

# 创建各节点
root            = Node('a')
root.left       = Node('b')
root.right      = Node('c')
root.left.left  = Node('d')
root.left.right = Node('e')
root.right.left = Node('f')
# 开始遍历
preorder(root)

改进 Node 的定义：

class Node:
    node_dict = {}    # 记录所有节点
    def __new__(cls, name, *args, **kwargs):
        """ 创建节点时，如果已存在同名节点，则返回其实例 """
        instance = cls.node_dict.get(name)
        if instance:
            return instance
        else:
            instance = super().__new__(cls)
            cls.node_dict[name] = instance
            return instance
    def __init__(self, name, data=None, left=None, right=None):
        self.name  = name
        self.data  = data
        self.left  = left
        self.right = right
    def __repr__(self):
        return "Node('{}')".format(self.name)

Node('a').left  = Node('b')
Node('a').right = Node('c')

• 这里的每个 Node 存放一条数据，只需指定节点的 name ，就可找到对应的 data 。
• 多个 Node 之间通过比较 name 的大小来排序。

排序

假设二叉树包含 n 个节点，用户想知道哪个节点的取值等于 v ，则有两种查询方案：

• 遍历所有节点，检查每个节点的值。时间复杂度为 O(n) 。
• 事先将二叉树中所有节点进行排序，然后按照二分法等方法，检查少量节点的值。耗时更短。

二叉树常见的几种排序算法：

• 二叉查找树（Binary Search Tree ，BST）

  • ：一种便于查找节点的二叉树，将所有节点中序排列，即：
    • 左子树的所有节点都小于父节点。
    • 右子树的所有节点都大于父节点。
  • 读取一个节点时，可以根据二分法快速定位，时间复杂度为 O(log n) 。
    • 插入、删除一个节点时，需要先根据二分法定位，然后移动中序的后继节点，比较麻烦。
  • 如果二叉查找树只存在一条路径，呈线性结构，则定位的时间复杂度为 O(n) 。
    • 使用 AVL tree 可以保证树的自平衡，避免这种情况。

• AVL tree

  • ：一种自平衡的二叉查找树。
  • 每个节点会记录自己的平衡因子，其值等于左子树的高度 - 右子树的高度，取值范围为 -1、0、1 。
  • 插入、删除节点时，通常需要进行左旋、右旋操作，移动节点的位置，从而维持平衡。

• B tree（B- Tree）

  • ：一种具有自平衡、查找特性的树，不属于二叉树 。特点如下：
    • 叶子结点都位于最底一层。
    • 假设树的阶数为 n ，则每个节点拥有 [n/2, n] 个子节点。
    • 每个节点存放最多 n-1 个数据元素。
      • 每个元素以 name:data 键值对形式存储，按升序排列。
      • 根节点可以只存放 1 个元素。
      • 叶子节点的元素数量等于子节点数减一，从而与子节点呈中序排列。
  • 与 AVL tree 相比，B tree 的每个节点存放更多元素，因此减少了节点数，减少了左旋、右旋操作，减少了磁盘 IO 。

• BPlus tree（B+ tree）

  • ：在 B tree 的基础上，增加定义：

    • 内部节点只存放元素 name ，用于索引。其完整的元素 name、data 存放在叶子节点，是叶子节点中的第一个元素。
    • 在最底一层，每个叶子节点会记录相邻的下一个叶子节点的指针，因此形成了线性结构，允许进行更快的顺序遍历。

  • 下图是一个 4 阶的 B+ tree ：

    

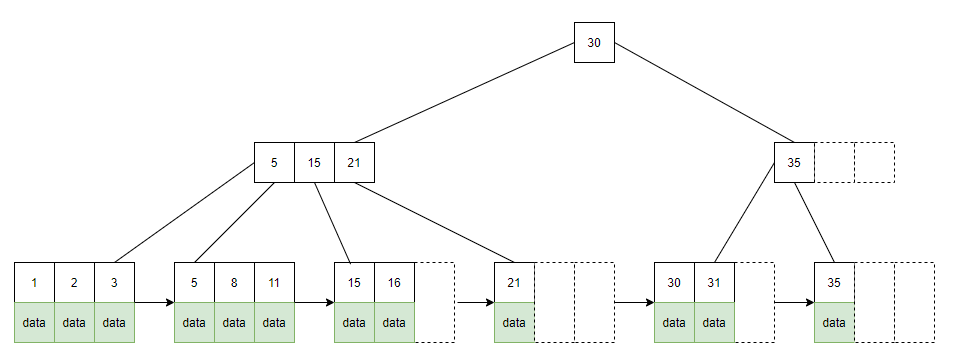
  • 例：B+ tree 的节点定义

    class BPTreeNode:
        def __init__(self, order):
            self.order      = order   # 记录树的阶数
            self.values     = []      # 一组元素的值
            self.keys       = []      # 一组元素的名称
            self.parent     = None    # 父节点
            self.children   = []      # 一组子节点
            self.next       = None    # 下一个叶子节点
            self.check_leaf = False   # 表示该节点是否为叶子节点
    

• 红黑树（Red-Black Tree，rbtree）

  • ：一种具有自平衡、查找特性的二叉树，采用较弱的平衡条件：
    • 叶子节点为空，只有内部节点存放数据元素。
    • 根节点、叶子节点总是黑色。
    • 其它内部节点可以是黑色或红色，只需要满足以下条件：
      • 每个红色节点的子节点都是黑色。
      • 对于任一节点，从该节点到其各个叶子节点，经过的黑色节点数相同。
  • 与 BST 相比，红黑树的平衡性保证了树中的最长路径不超过最短路径的两倍，因此查找耗时更稳定。
  • 与 AVL tree 相比，红黑树的平衡性较弱，减少了左旋、右旋操作，因此开销更低。

字典树

• 字典树，又称为前缀树、trie ，是一种对多个单词进行排序的方案。

• 原理：

  • 将前缀相同的各个单词，存放在树的同一条路径上。
  • 除了根节点以外，每个节点存放一个字母。
  • 每个节点可以有任意个子节点，每个子节点存放的字母不同。
  • 使用单词的存放路径作为 key ，查找单词的 value 。
  • 树的高度等于最长的一个单词的长度。假设树的高度为 n ，则查找一个单词的时间复杂度为 O(n) 。

• 如下图：

  

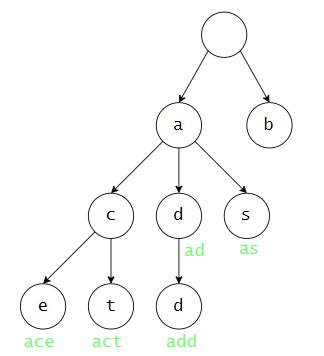
图

• 一个图形结构，包含多个节点。这些节点在逻辑上散乱放置。

  • 任意两个节点之间都可以用一条边连接，代表建立联系，称为相邻。

• 从定义上看，线性结构 < 树形结构 < 图形结构

  • 线性结构，是树形结构的一种。如果树形结构中只存在一条路径，则会成为线性结构。
  • 树形结构，是图形结构的一种。如果图形结构中所有节点分层放置，则会成为树形结构。

哈希表

• 一个哈希表（hash table），包含多个节点。每个节点包含 key、value 两条数据，称为键、值。

  • 当用户新增一个节点时，哈希表会计算 key 的哈希值，从而决定该节点的存储地址。然后将 key、value 存储在该地址。
  • key 通常是字符串类型，从而方便计算哈希值。而 value 可以是任意数据类型。

• 特点：

  • 哈希表有些像链表，可以存储任意个元素，可以随时增加、删除元素。但链表只能按顺序遍历各个元素，而哈希表知道每个元素的存储地址，可以直接读写任一元素，时间复杂度为 O(1) 。
  • 哈希表有些像图形结构，所有节点散乱存放。但哈希表中，没有节点之间存在联系。

• 例如用数组，可以实现一个哈希表：

  1. 创建一个数组，可以容纳 capacity 个节点。
  2. 当用户新增一个节点时，计算 hash(key) 。
  3. 计算 index = hash(key) % capacity ，然后将该节点存储为数组的第 index 个元素。

• 如果两个节点的哈希值相同，则会存储在相同地址。

  • 为了减少碰撞，可以将 capacity 设置得很大，比节点总数大几倍。
  • 发生碰撞时，可以创建一个 capacity 更大的哈希表，然后将所有节点拷贝写入新表。这称为哈希扩容。
  • 哈希扩容的耗时较久。另一种方案是，允许多个节点存储在相同地址，将它们组成一个链表。